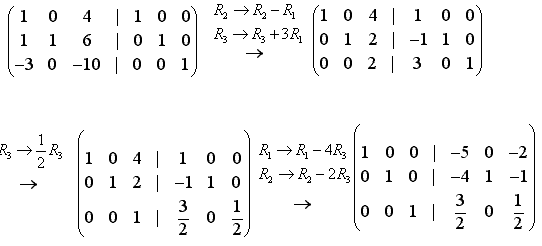Základní operace s maticemi
Sčítání a odčítání matic
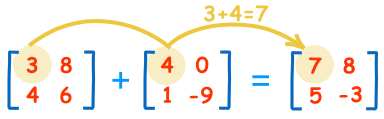
Nutnou podmínkou pro sčítání nebo odčítání dvou matic je jejich velikost, přičemž abychom mohli tuto operaci vůbec provádět, je potřeba mít obě vstupní matice o stejné velikosti m×n. Nelze tedy sčítat ani od sebe odčítat dvě matice o nesouhlasném počtu řádků nebo sloupců.
Sama operace je potom již jednoduchá. Každý prvek sečteme resp. odečteme s prvkem druhé matice na stejné pozici (i,j). Z toho vyplívá, že výsledná matice má opět stejný počet řádků i sloupců.
Násobení
Násobení je o něco komplikovanější. U této operace již není vyžadováno, aby obě matice byly "tvarově" totožné, přesto zde platí jednoznačná pravidla. Vstupní matice mohou být buďto čtvercové, přičemž u těchto není potřeba řešit řádky ani sloupce, nebo mohou být libovolného obdélníkového tvaru. Důležitou podmínkou je, že počet sloupců první matice musí být roven počtu řádků druhé matice. Tady pozor, násobení není komutativní záležitost a tak A⋅B != B⋅A. To souvisí se způsobem, jakým se matice mezi sebou násobí.
Maticové násobení probíhá následujícím způsobem:
- Každý prvek prvního řádku první matice vynásobíme s každým prvkem prvního sloupce druhé matice a jejich součet zapíšeme do výsledné matice do prvního řádku a prvního slouce.
- Pro výpočet dalšího prvku, třeba ve druhém sloupci a prvním řádku, zvolíme první řádek první matice a druhý sloupec druhé matice.
- Obdobně je tomu u druhého řádku a prvního sloupce výsledné matice, přičemž v tomto případě mezi sebou násobíme prvky druhého řádku první matice a prvního sloupce druhé matice
Tento postup opakujeme do té doby, dokud nevypočteme všechny prvky výsledné matice, jejíž celkové konečné rozměry jsou rovny počtu řádků první matice × počtu sloupců druhé matice.
U matic lze provádět také násobení matice konstantou.
Inverzní matice
U matic neexistuje něco jako dělení. Hojně se ale využívá inverzních matic, pro než platí, A⋅A-1 = E = A-1⋅A.
Z matice A vynásobené maticí A-1 vznikne jednotková matice E.
K jejich nalezení existuje několik cest, z nichž nejuniverzálnější je prováděna skrze jednotkovou matici E a postupný převod pomocí Gaussovy eliminační metody (viz. níže na stránce).
Matice 2×2
Nejsnazším způsobem, vhodným ale jen pro matice typu 2×2, je výpočet determinantu následujícím způsobem.
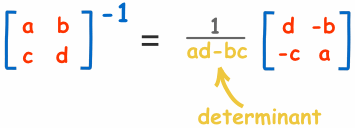
Na konkrétním příkladě to vypadá takto
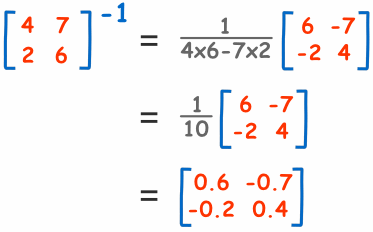
Obecný postup přes jednotkovou matici
Protože ale tento přístup pro větší matice nefunguje, je vhodné být seznámen také s další metodou, která využívá zápisu původní a jednotkové matice vedle sebe. Postupnými úpravami přes Gaussovu eliminační metodu je poté snahou dospět na místě původní matice k jednotkové matici. Důsledkem této úpravy je vznik kýžené inverzní matice na místě původní jednotkové matice.
