Lineární algebra » Důležité definice
Základy, bez kterých se neobejdete
- Lineární kombinace
- Uvažujeme vektorový prostor V nad tělesem T. Dále nechť je vektor x z vektorového prostoru V nějaký vektor a x1, x2, … xn je soubor n vektorů z vektorového prostoru V. Potom říkáme, že vektor x je lineární kombinací vektorů x1, x2, … xn, právě tehdy když existuje n-tice čísel a1, a2, … an z tělesa T, že lze vektor x vyjádřit ve tvaru
-
x = a1⋅x1 + a2⋅x2 + … + an⋅xn,
kde číslům ai říkáme koeficienty lineární kombinace. Jsou-li všechny koeficienty ai nulové, je lineární kombinace označována jako triviální. Takováto lineární kombinace je bez ohledu na hodnotu vektorů x1, x2, … xn vždy rovna nulovému vektoru. Je-li alespoň jeden z koeficientů ai různý od nuly, pak říkáme, že je lineární kombinace netriviální. - Lineární nezávislost (LN) a Lineární závislost (LZ)
- Buď V vektorový prostor nad tělesem T a mějme dále soubor vektorů x1, … , xk z V pro jisté přirozené číslo k ≥ 1. Uvažujme pak všechny možné lineární kombinace tohoto souboru vektorů, které jsou rovny nulovému vektoru. Pak říkáme, že soubor x1, …, xk je lineárně nezávislý, právě když ze všech lineárních kombinací těchto vektorů je rovna nulovému vektoru jen triviální lineární kombinace. V opačném případě nazýváme soubor výše lineárně závislý. Pro lineární nezávislost se běžně používá zkratka LN a pro lineární závislost zkratka LZ.
- Zjednodušeně lze říci, že je-li libovolný vektor z celého souboru násobkem jiného nebo je nulový, jedná se o soubor lineárně závislý (LZ).
- Matice
- Matice je v matematice obdélníkové či čtvercové schéma matematických objektů – prvků matice z tělesa T. Obsahuje obecně m řádků a n sloupců. Hovoříme pak o matici typu m × n.
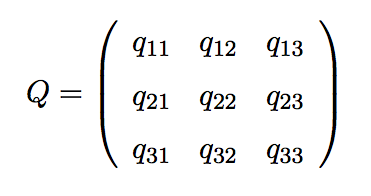
- Sčítat a odečítat lze pouze matice o stejné velikosti.
- Libovolnou matici lze vynásobit libovolnou nenulovou konstantou aniž by se změnil stav samotné matice.
- Násobit matice lze pouze v případě, že matice vlevo má stejný počet spoupců jako je počet řádků matice vpravo.
- Násobení matic není komutativní záležitost a tak A⋅B ≠ B⋅A
- Matice nelze dělit, ale lze je převést na inverzí tvar. Platí vztah A⋅A-1 = A-1⋅A = E
- Čtvercová matice
- Je matice, která má stejný počet řádků jako sloupců.
- Inverzní matice
- Inverzní matice k dané matici je taková matice, která po vynásobení s původní maticí dá jednotkovou matici.
- Transponovaná matice
- Matice, která vznikne z matice A vzájemnou výměnou řádků a sloupců. Označujeme ji AT.
- Determinant matice
- V lineární algebře je determinant zobrazení, které přiřadí každé čtvercové matici A skalár det A.
- Determinantem čtvercové matice řádu n nazýváme součet všech součinů n prvků této matice takových, že v žádném z uvedených součinů se nevyskytují dva prvky z téhož řádku ani z téhož sloupce.
- Hodnost matice
- Hodnost matice je číslo, které představuje počet nezávislých řádků nebo sloupců matice. Lze ji určit např. gaussovou eliminací. Po provedení eliminace je hodnost matice rovna počtu nenulových řádků nebo také počtu hlavních sloupců (řádků).