Maticové rovnice

Předpoklady

Pro výpočet maticových rovnic je důležité vědět, že u násobení matic neplatí komutativita násobení.
Tj, obecně pro matice neplatí A⋅B = B⋅A.

Speciální případ matic je matice jednotková, u které je možné se na komutativitu spolehnout a tak vždy platí A⋅E = E⋅A. Dále je zřejmý vztah E = A⋅A-1 = A-1⋅A.

Z tohoto důvodu je nutné při úpravách maticových rovnic zachovávat pořadí jednotlivých matic a není možné je bez úvahy prohazovat. Platí tedy, že A⋅A-1⋅B = E⋅B = B, ale A⋅B⋅A-1 již není rovno B.

Příklady maticových rovnic

  1. A⋅X = B
    A-1⋅A⋅X = A-1⋅B
    X = A-1⋅B

  2. X⋅B + C = A
    X⋅B = A - C
    D = A - C
    X⋅B = D
    X⋅B⋅B-1 = D⋅B-1
    X = D⋅B-1

  3. 3⋅A + X⋅B = E + 2⋅X
    X⋅B - 2⋅X = E - 3⋅A
    C = E - 3⋅A
    X⋅(B - 2⋅E) = C
    D = B - 2⋅E
    X⋅D = C
    X⋅D⋅D-1 = C⋅D-1
    X = C⋅D-1

  4. 2⋅X + 4⋅E - 2⋅B = A⋅X + B
    4⋅E - 3⋅B = A⋅X - 2⋅X
    C = 4⋅E - 3⋅B
    C = (A - 2⋅E)⋅X
    D = A - 2⋅E
    C = D⋅X
    D-1⋅C = D-1⋅D⋅X
    D-1⋅C = X

Ukázka jednoduchého výpočtu

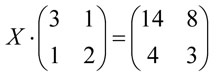
matrix_example

X⋅A = B
X⋅A⋅A-1 = B⋅A-1
X = B⋅A-1
Po dosazení matic a jejich výpočtu dostaneme výsledek X = 8.