Lineární algebra » Výpočet determinantu

Výpočet determinantu

Gaussova eliminační metoda (GEM)

Gaussova metoda spočívá v provedení takových úprav matice, které nemění hodnotu determinantu, ale zjednoduší výpočet jeho hodnoty. Cílem prováděných úprav je získat trojúhelníkovou matici A (tedy pro i > j je a_ij = 0), neboť pro tu platí

det A = a₁₁⋅a₂₂ … a_nn,

tzn. determinant trojúhelníkové matice je roven součinu prvků na hlavní diagonále matice.

Při úpravách matice pro výpočet determinantu postupujeme podle těchto pravidel:

Pokud B vznikne z A výměnnou dvou sloupců potom det B = -det A
Pokud B vznikne z A vynásobením řádku nebo sloupce skalárem c, potom det B = c⋅det A
Pokud B vznikne z A přičtením násobku jednoho řádku k jinému, nebo přidáním násobku sloupce k jinému sloupci potom det B = det A

Opakovaným použitím uvedených pravidel převedeme matici na matici trojúhelníkovou a pro tu poté snadno spočteme determinant.

Příklad

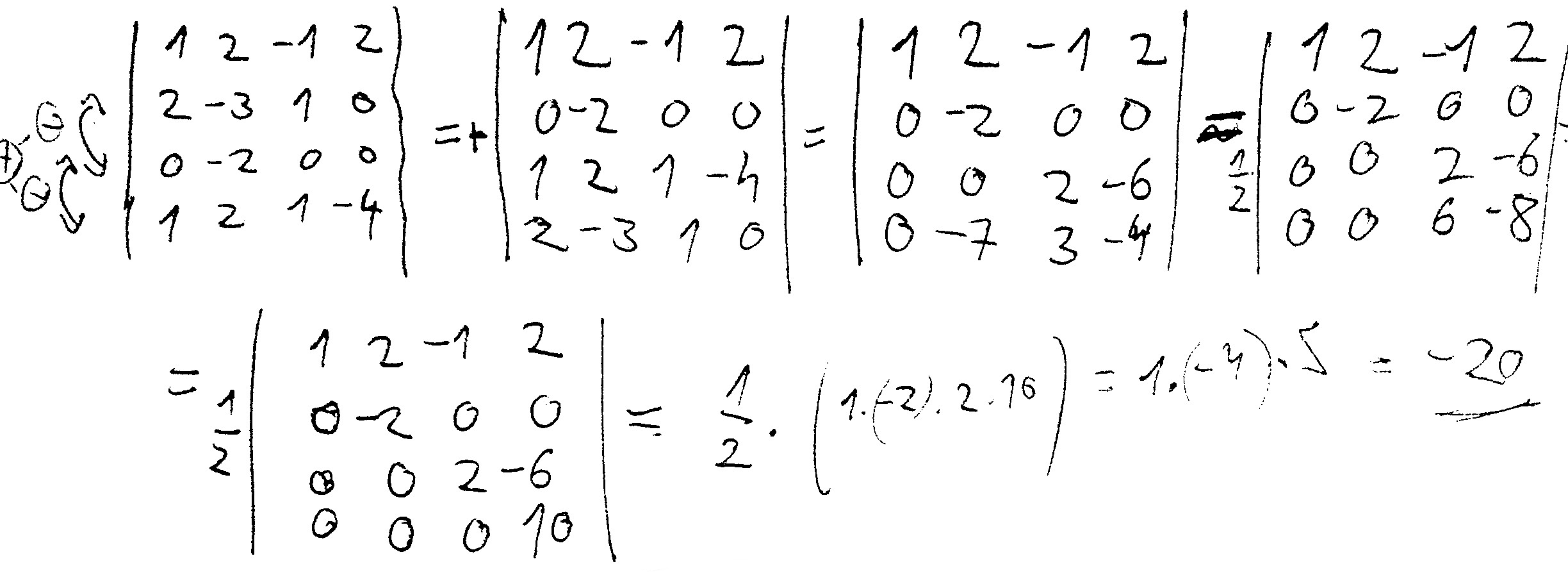
Způsoby výpočtu determinantů s menším počtem řádků

Nechť A = a_ij je čtvercová matice.

Matice řádu 1

Pokud A je matice 1×1, je
det A = a₁₁
Determinant matice prvního řádu je tedy roven hodnotě jediného prvku této matice.

Matice řádu 2

Pokud A je matice 2×2, je
det A = a₁₁⋅a₂₂ - a₂₁⋅a₁₂

Matice řádu 3

Pro matici A typu 3×3 je vzorec složitější:
det A = a₁₁⋅a₂₂⋅a₃₃ + a₁₃⋅a₂₁⋅a₃₂ + a₁₂⋅a₂₃⋅a₃₁ - a₁₃⋅a₂₂⋅a₃₁ - a₁₁⋅a₂₃⋅a₃₂ - a₁₂⋅a₂₁⋅a₃₃

Stručně slovy se jedná o součet násobků vždy tří prvků a to z hlavní diagonály + dvou prvků přilehlých hlavní diagonále ⋅ prvek v protiléhlém rohu + dalších dvou prvků přilehlých hlavní diagonále z druhé strany ⋅ prvek v protilehlém rohu - (totéž jako první část jen se vše odvíjí od vedlejší diagonály).

Mnemotechnická pomůcka sloužící k zapamatování postupu výpočtu determinantu třetího řádu se nazývá Sarrusovo pravidlo.

Laplaceův rozvoj

Pomocí této metody můžeme rozvinout determinant podle řádku či podle sloupce, což je pro relativně malé matice celkem efektivní metoda. Například podle řádku i
det A = ∑_j=1ⁿ a_ij⋅C_ij
kde C_ij jsou kofaktory, tedy C_ij je (-1)^i+j krát determinant matice, která vznikne z A odstraněním i-tého řádku a j-tého sloupce. Takováto matice se nazývá submatice a determinant k ní příslušný subdeterminant. Ze vzorce je zřejmé, že je nejvhodnější využívat k rozvinutí řádek nebo sloupec, který obsahuje hodně 0.

Nebo také zjednodušeně det A = (-1)^i+j⋅det A_i,j, kde det A_i,j obsahuje všechny prvky původní matice bez řádku a sloupce, v níž byl původně odebraný prvek.

Příklad